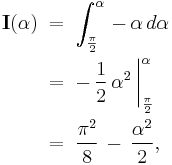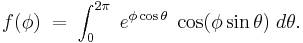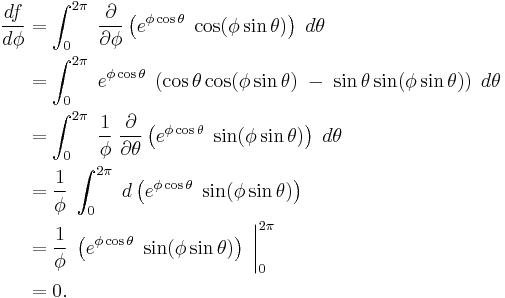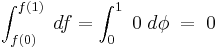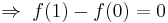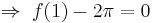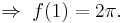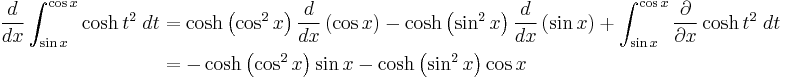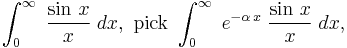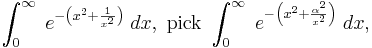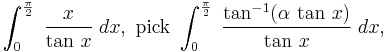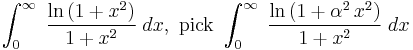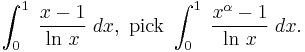Differentiation under the integral sign
Differentiation under the integral sign is a useful operation in calculus. Suppose that it is required to differentiate with respect to x the function
where the functions 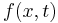 and
and 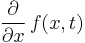 are both continuous in both
are both continuous in both 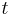 and
and 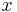 in some region of the
in some region of the 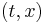 plane, including
plane, including 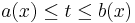 ,
, 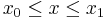 , and the functions
, and the functions 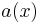 and
and 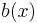 are both continuous and both have continuous derivatives for
are both continuous and both have continuous derivatives for 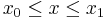 . Then for
. Then for 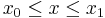 :
:
This formula is the general form of the Leibniz integral rule and can be derived using the fundamental theorem of calculus. The fundamental theorem of calculus is just a particular case of the above formula, for 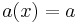 , a constant,
, a constant, 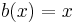 and
and 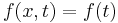 .
.
If both upper and lower limits are taken as constants, then the formula takes the shape of an operator equation:
where 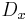 is the partial derivative with respect to
is the partial derivative with respect to 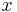 and
and 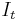 is the integral operator with respect to
is the integral operator with respect to 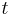 over a fixed interval. That is, it is related to the symmetry of second derivatives, but involving integrals as well as derivatives. This case is also known as the Leibniz integral rule.
over a fixed interval. That is, it is related to the symmetry of second derivatives, but involving integrals as well as derivatives. This case is also known as the Leibniz integral rule.
The following three basic theorems on the interchange of limits are essentially equivalent:
- the interchange of a derivative and an integral (differentiation under the integral sign; i.e., Leibniz integral rule)
- the change of order of partial derivatives
- the change of order of integration (integration under the integral sign; i.e., Fubini's theorem)
Contents |
Higher dimensions
The Leibniz integral rule can be extended to multidimensional integrals. In two and three dimensions, this rule is better known from the field of fluid dynamics as the Reynolds transport theorem:
where 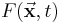 is a scalar function,
is a scalar function, 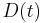 and
and 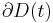 denote a time-varying connected region of
denote a time-varying connected region of 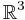 and its boundary, respectively,
and its boundary, respectively, 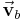 is the Eulerian velocity of the boundary (see Lagrangian and Eulerian coordinates) and
is the Eulerian velocity of the boundary (see Lagrangian and Eulerian coordinates) and 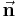 is unit outwards normal.
is unit outwards normal.
The general statement of the Leibniz integral rule requires concepts from differential geometry, specifically differential forms, exterior derivatives, wedge products and interior products. With those tools, the Leibniz integral rule in 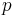 -dimensions is:[1]
-dimensions is:[1]
where 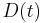 is a time-varying domain of integration,
is a time-varying domain of integration, 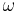 is a
is a 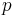 -form,
-form, 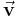 is the vector field of the velocity,
is the vector field of the velocity, 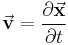 ,
, 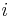 denotes the interior product,
denotes the interior product, 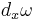 is the exterior derivative of
is the exterior derivative of 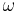 with respect to the space variables only and
with respect to the space variables only and 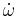 is the time-derivative of
is the time-derivative of 
Derivation of the principle of differentiation under the integral sign
A definite integral is a function of its upper limit 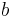 and its lower limit
and its lower limit 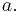
If 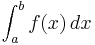 is a continuous function of
is a continuous function of 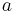 or
or 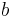 , then, from the definition of the definite integral,
, then, from the definition of the definite integral, 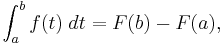
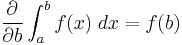 and
and 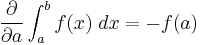
since, from proof of the fundamental theorem of calculus,
Suppose 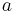 and
and 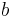 are constant, and that
are constant, and that 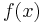 involves a parameter
involves a parameter 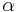 which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,
which is constant in the integration but may vary to form different integrals. Then, by the definition of a function,
In general, this may be differentiated by differentiating under the integral sign; i.e.,
To prove this and, at the same time, to determine conditions under which the formula is true, we proceed as follows:
From 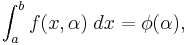
From the fact that ![\int_a^b f_1(x)\;dx%2B\int_a^b f_2(x)\;dx=\int_a^b[f_1(x)%2Bf_2(x)]\;dx,](/2012-wikipedia_en_all_nopic_01_2012/I/769473786a75d16fc26a3ae23e3b1338.png) we have
we have
If 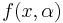 is a continuous function of
is a continuous function of 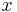 and
and 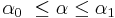 when
when 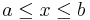 then for any
then for any 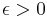 there exists
there exists 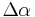 such that
such that
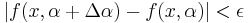 for all values of
for all values of ![x\in[a,b].](/2012-wikipedia_en_all_nopic_01_2012/I/f4385490b1258f3a845e89968e880d59.png)
(This follows from the Heine–Cantor theorem that every continuous function on a compact set is uniformly continuous.)
Therefore, from 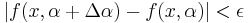 and
and ![\Delta \phi=\int_a^b[f(x,\alpha%2B\Delta\alpha)-f(x,\alpha)]\;dx,\,](/2012-wikipedia_en_all_nopic_01_2012/I/51a09b230092af7a277220419ff96185.png)
we get 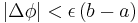 and the fact that
and the fact that 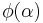 is, therefore, a continuous function.
is, therefore, a continuous function.
Similarly if 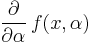 exists and is continuous, then for all
exists and is continuous, then for all 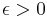 there exists
there exists 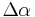 such that:
such that:
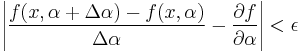 for all
for all ![x\in[a,b].](/2012-wikipedia_en_all_nopic_01_2012/I/f4385490b1258f3a845e89968e880d59.png)
Therefore,
Now, 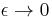 as
as 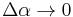 , therefore,
, therefore,
This is the formula we set out to prove.
Now, suppose 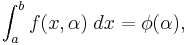 where
where 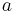 and
and 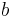 are functions of
are functions of 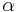 which take increments
which take increments 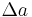 and
and 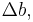 respectively, when
respectively, when 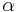 is increased by
is increased by 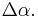 Then,
Then,
A form of the mean value theorem, 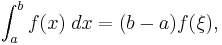 where
where 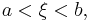 can be applied to the first and last integrals of the formula for
can be applied to the first and last integrals of the formula for 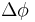 above, resulting in
above, resulting in
Dividing by 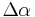 , letting
, letting 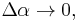 noticing
noticing 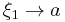 and
and 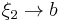 and using the result
and using the result 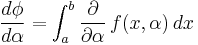 yields
yields
This is the general form of the Leibniz integral rule.
Examples
Example 1
If 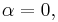
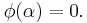
If 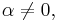
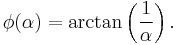
The function 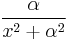 is not continuous at the point
is not continuous at the point  and the function
and the function 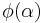 has a discontinuity at
has a discontinuity at 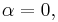 because
because 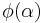 approaches
approaches 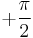 as
as 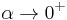 and approaches
and approaches 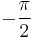 as
as 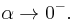
If we now differentiate 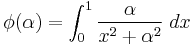 with respect to
with respect to 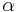 under the integral sign, we get
under the integral sign, we get
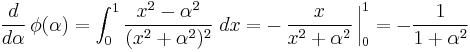 ,
,
which is, of course, true for all values of 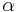 except
except 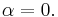
Example 2
The principle of differentiating under the integral sign may sometimes be used to evaluate a definite integral.
Consider integrating 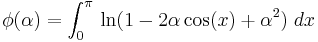 (for
(for 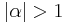 ).
).
Now,
As 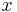 varies from
varies from 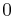 to
to 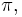
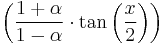 varies through positive values from
varies through positive values from 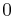 to
to 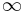 when
when 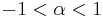 and
and 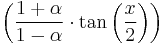 varies through negative values from
varies through negative values from 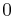 to
to 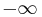 when
when 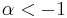 or
or 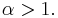
Hence,
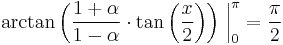 when
when 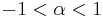
and
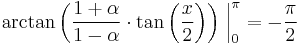 when
when 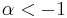 or
or 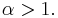
Therefore,
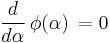 when
when 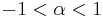 and
and
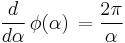 when
when 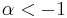 or
or 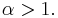
Upon integrating both sides with respect to 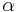 , we get
, we get 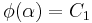 when
when 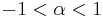 and
and 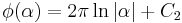 when
when 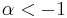 or
or 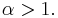
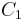 may be determined by setting
may be determined by setting 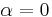 in
in
Thus, 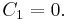 Hence,
Hence, 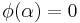 when
when 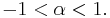
To determine 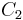 in the same manner, we should need to substitute in
in the same manner, we should need to substitute in 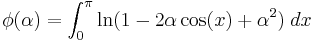 a value of
a value of 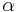 greater numerically than 1. This is somewhat inconvenient. Instead, we substitute
greater numerically than 1. This is somewhat inconvenient. Instead, we substitute 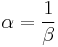 , where
, where 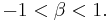 Then,
Then,
Therefore, 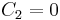 (and
(and 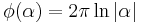 when
when 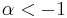 or
or 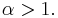 )
)
The definition of 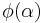 is now complete:
is now complete:
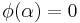 when
when 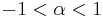 and
and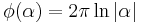 when
when 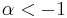 or
or 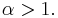
The foregoing discussion, of course, does not apply when 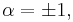 since the conditions for differentiability are not met.
since the conditions for differentiability are not met.
Example 3
Here, we consider the integration of
where both 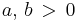 , by differentiating under the integral sign.
, by differentiating under the integral sign.
Let us first find 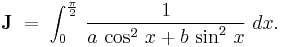
Dividing both the numerator and the denominator by 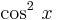 yields
yields
The limits of integration being independent of 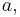
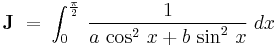 gives us
gives us
whereas 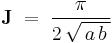 gives us
gives us
Equating these two relations then yields
In a similar fashion, pursuing 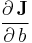 yields
yields
Adding the two results then produces
which is the value of the integral 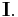
Note that if we define
it can easily be shown that
Given 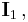 this partial-derivative-based recursive relation (i.e., integral reduction formula) can then be utilized to compute all of the values of
this partial-derivative-based recursive relation (i.e., integral reduction formula) can then be utilized to compute all of the values of 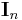 for
for 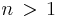 (
(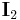 ,
, 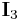 ,
, 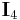 etc.).
etc.).
Example 4
Here, we consider the integral
for 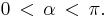
Differentiating under the integral with respect to 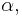 we have
we have
Now, when 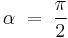 , we have, from
, we have, from 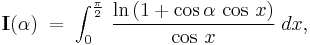
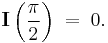
Hence,
which is the value of the integral 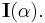
Example 5
Here, we consider the integral 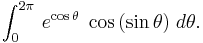
We introduce a new variable 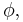 and rewrite the integral as
and rewrite the integral as
Note that for 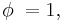
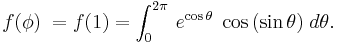
Thus, we proceed
From the equation for 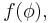 we can see
we can see 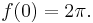 So, integrating both sides of
So, integrating both sides of 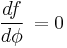 with respect to
with respect to 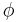 between the limits
between the limits 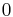 and
and 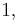 yields
yields
which is the value of the integral 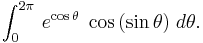
Example 6
Here is an example that has variable limits. Let us try to find 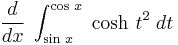 . In this example, we shall simply apply the above given formula, to get
. In this example, we shall simply apply the above given formula, to get
where the derivative with respect to x of hyperbolic cosine t squared is 0. This is a simple example on how to use this formula for variable limits.
Other problems
There are innumerable other integrals that can be solved "quickly" using the technique of differentiation under the integral sign. For examples, to solve
and for
Popular culture
- Differentiation under the integral sign is mentioned in the late physicist Richard Feynman's best-selling memoir Surely You're Joking, Mr. Feynman! (in the chapter "A Different Box of Tools"), where he mentions learning it from an old text, Advanced Calculus (1926), by Frederick S. Woods (who was a professor of mathematics in the Massachusetts Institute of Technology) while in high school. The technique was not often taught when Feynman later received his formal education in calculus and, knowing it, Feynman was able to use the technique to solve some otherwise difficult integration problems upon his arrival at graduate school at Princeton University. The direct citation from Surely You're Joking, Mr. Feynman! regarding the method of differentiation under the integral sign is as follows:
One thing I never did learn was contour integration. I had learned to do integrals by various methods shown in a book that my high school physics teacher Mr. Bader had given me.One day he told me to stay after class. "Feynman," he said, "you talk too much and you make too much noise. I know why. You're bored. So I'm going to give you a book. You go up there in the back, in the corner, and study this book, and when you know everything that's in this book, you can talk again." So every physics class, I paid no attention to what was going on with Pascal's Law, or whatever they were doing. I was up in the back with this book: Advanced Calculus, by Woods. Bader knew I had studied Calculus for the Practical Man a little bit, so he gave me the real works—it was for a junior or senior course in college. It had Fourier series, Bessel functions, determinants, elliptic functions—all kinds of wonderful stuff that I didn't know anything about. That book also showed how to differentiate parameters under the integral sign—it's a certain operation. It turns out that's not taught very much in the universities; they don't emphasize it. But I caught on how to use that method, and I used that one damn tool again and again. So because I was self-taught using that book, I had peculiar methods of doing integrals.
The result was, when guys at MIT or Princeton had trouble doing a certain integral, it was because they couldn't do it with the standard methods they had learned in school. If it was contour integration, they would have found it; if it was a simple series expansion, they would have found it. Then I come along and try differentiating under the integral sign, and often it worked. So I got a great reputation for doing integrals, only because my box of tools was different from everybody else's, and they had tried all their tools on it before giving the problem to me.
See also
References
- ^ Flanders, Harley (June–July 1973). "Differentiation under the integral sign". American Mathematical Monthly 80 (6): 615–627. doi:Article Link on JSTOR
- "Advanced Calculus", Frederick S. Woods, Ginn and Company, 1926.
- "Advanced Calculus", David V. Widder, Dover Publications Inc., New Ed edition (Jul 1990).
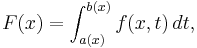
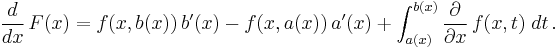
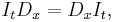
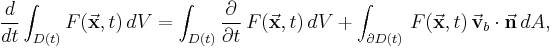
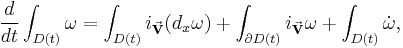
![\begin{align}
\frac{\partial}{\partial b}\int_a^b f(x)\; dx
&= \lim_{\Delta b \to 0} \frac{1}{\Delta b} \left[ \int_a^{b%2B\Delta b} f(x)\,dx - \int_a^b f(x)\,dx \right]
\\
&= \lim_{\Delta b \to 0} \frac{1}{\Delta b} \int_b^{b%2B\Delta b} f(x)\,dx
= \lim_{\Delta b \to 0} \frac{1}{\Delta b} \left[ f(b)\, \Delta b %2B \mathcal{O}\left(\Delta b^2\right) \right]
\\
&= f(b)
\qquad \text{and}
\\
\frac{\partial}{\partial a}\int_a^b f(x)\; dx
&= \lim_{\Delta a \to 0} \frac{1}{\Delta a} \left[ \int_{a%2B\Delta a}^b f(x)\,dx - \int_a^b f(x)\,dx \right]
\\
&= \lim_{\Delta a \to 0} \frac{1}{\Delta a} \int_{a%2B\Delta a}^a f(x)\,dx
= \lim_{\Delta a \to 0} \frac{1}{\Delta a} \left[ -f(a)\, \Delta a %2B \mathcal{O}\left(\Delta a^2\right) \right]
\\
&= -f(a).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/2267c8d55e2be4198f9c25d96e21b9c5.png)
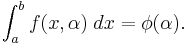
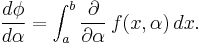
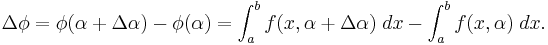
![\Delta\phi=\int_a^b f(x,\alpha%2B\Delta\alpha)\;dx-\int_a^b f(x,\alpha)\;dx=\int_a^b[f(x,\alpha%2B\Delta\alpha)-f(x,\alpha)]\;dx.\,](/2012-wikipedia_en_all_nopic_01_2012/I/2a018ab0e6f873925f244f1aec3609a3.png)
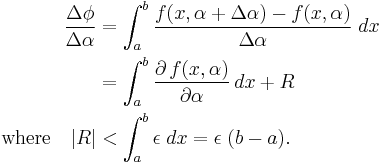
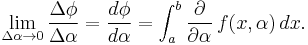
![\begin{align}
\Delta\phi
&=\phi(\alpha%2B\Delta\alpha)-\phi(\alpha)=\int_{a%2B\Delta a}^{b%2B\Delta b}f(x,\alpha%2B\Delta\alpha)\;dx\,-\int_a^b f(x,\alpha)\;dx\,
\\
&=\int_{a%2B\Delta a}^af(x,\alpha%2B\Delta\alpha)\;dx%2B\int_a^bf(x,\alpha%2B\Delta\alpha)\;dx%2B\int_b^{b%2B\Delta b}f(x,\alpha%2B\Delta\alpha)\;dx\,-\int_a^b f(x,\alpha)\;dx\,
\\
&=-\int_a^{a%2B\Delta a}\,f(x,\alpha%2B\Delta\alpha)\;dx%2B\int_a^b[f(x,\alpha%2B\Delta\alpha)-f(x,\alpha)]\;dx%2B\int_b^{b%2B\Delta b}\,f(x,\alpha%2B\Delta\alpha)\;dx.\,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/56c20aebe9358d6b2149a0b491f73431.png)
![\Delta\phi=-\Delta a\,f(\xi_1,\alpha%2B\Delta\alpha)%2B\int_a^b[f(x,\alpha%2B\Delta\alpha)-f(x,\alpha)]\;dx%2B\Delta b\,f(\xi_2,\alpha%2B\Delta\alpha).\,](/2012-wikipedia_en_all_nopic_01_2012/I/6d53e26999e77d87415226e7402b8507.png)
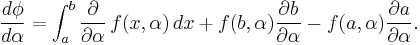
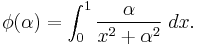
![\begin{align}
\frac{d}{d\alpha}\,\phi(\alpha)\,
&=\int_0^\pi \frac{-2\cos(x)%2B2\alpha}{1-2\alpha \cos(x)%2B\alpha^2}\;dx\,
\\[8pt]
&=\frac{1}{\alpha}\int_0^\pi\,\left(1-\frac{(1-\alpha)^2}{1-2\alpha \cos(x)%2B\alpha^2}\,\right)\,dx\,
\\[8pt]
&=\frac{\pi}{\alpha}-\frac{2}{\alpha}\left\{\,\arctan\left(\frac{1%2B\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\right\}\,\bigg|_0^\pi.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/7f2c3f58654cc8cf37f0b1e978b7acb8.png)
![\begin{align}
\phi(\alpha) &= \int_0^\pi \ln(1-2\alpha \cos(x)%2B\alpha^2)\;dx. \\[6pt]
\phi(0)
&=\int_0^\pi \ln(1)\;dx\,
\\[6pt]
&=\int_0^\pi 0\;dx\,
\\[6pt]
&=0\,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/890eee0adc43d255d64b18f5d2785721.png)
![\begin{align}
\phi(\alpha)
&=\int_0^\pi\left(\ln(1-2\beta \cos(x)%2B\beta^2)-2\ln|\beta|\right)\;dx\,
\\[8pt]
&=0-2\pi\ln|\beta|\,
\\[8pt]
&=2\pi\ln|\alpha|\,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/20d9a341db881186cb98d24931d68c1b.png)
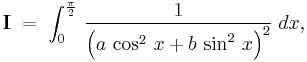
![\begin{align}
\textbf J\;
&=\;\int_0^{\frac{\pi}{2}}\,\frac{\sec^2\,x}{a\,%2Bb\,\tan^2\,x}\;dx
\\[6pt]
&=\,\frac{1}{b}\,\int_0^{\frac{\pi}{2}}\,\frac{1}{\left(\sqrt{\,\frac{a}{b}\,}\right)^2%2B\tan^2\,x}\;d(\tan\,x)\,
\\[6pt]
&=\,\frac{1}{\sqrt{\,a\,b\,}}\,\left(\tan^{-1}\left(\sqrt{\,\frac{b}{a}\,}\,\tan\,x\right)\right)\,\bigg|_0^{\frac{\pi}{2}}\;=\;\frac{\pi}{2\,\sqrt{\,a\,b\,}}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/ebbd6b45161cf6c5a5382d700fdb2377.png)
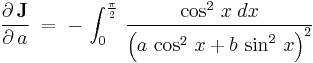
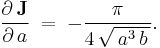
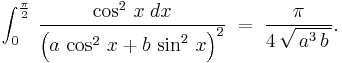
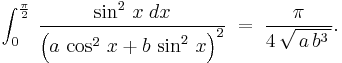
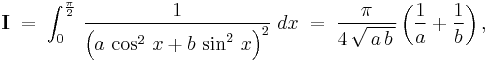
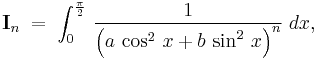
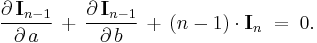
![\begin{align}
\frac{d}{d\alpha}\,\textbf I(\alpha)\;
&=\;\int_0^{\frac{\pi}{2}}\,\frac{\partial}{\partial\alpha}\,\left(\frac{\ln\,(1\,%2B\,\cos\alpha\,\cos\,x)}{\cos\,x}\right)\,dx\,
\\
&=\;-\,\int_0^{\frac{\pi}{2}}\,\frac{\sin\alpha}{1%2B\cos\alpha\,\cos\,x}\,dx\,
\\
&=\;-\,\int_0^{\frac{\pi}{2}}\,\frac{\sin\alpha}{\left(\cos^2\,\frac{x}{2}%2B\sin^2\,\frac{x}{2}\right)\,%2B\,\cos\alpha\,\left(\cos^2\,\frac{x}{2}-\sin^2\,\frac{x}{2}\right)}\,dx\,
\\
&=\;-\,\frac{\sin\alpha}{1-\cos\alpha}\,\int_0^{\frac{\pi}{2}}\,\frac{1}{\cos^2\,\frac{x}{2}}\,\frac{1}{\left[\,\left(\frac{1%2B\cos\alpha}{1-\cos\alpha}\right)\,%2B\,\tan^2\,\frac{x}{2}\,\right]}\,dx\,
\\
&=\;-\,\frac{2\,\sin\alpha}{1-\cos\alpha}\,\int_0^{\frac{\pi}{2}}\,\frac{\frac{1}{2}\,\sec^2\,\frac{x}{2}}{\left[\,\left(\frac{2\,\cos^2\,\frac{\alpha}{2}}{2\,\sin^2\,\frac{\alpha}{2}}\right)\,%2B\,\tan^2\,\frac{x}{2}\,\right]}\,dx\,
\\
&=\;-\,\frac{2\left(2\,\sin\,\frac{\alpha}{2}\,\cos\,\frac{\alpha}{2}\right)}{2\,\sin^2\,\frac{\alpha}{2}}\,\int_0^{\frac{\pi}{2}}\,\frac{1}{\left[\,\left(\frac{\cos\,\frac{\alpha}{2}}{\sin\,\frac{\alpha}{2}}\right)^2\,%2B\,\tan^2\,\frac{x}{2}\,\right]}\,d\left(\tan\,\frac{x}{2}\right)\,
\\
&=\;-\,2\,\cot\,\frac{\alpha}{2}\,\int_0^{\frac{\pi}{2}}\,\frac{1}{\left[\,\cot^2\,\frac{\alpha}{2}\,%2B\,\tan^2\,\frac{x}{2}\,\right]}\,d\left(\tan\,\frac{x}{2}\right)\,
\\
&=\;-\,2\,\left(\tan^{-1}\,\left(\tan\,\frac{\alpha}{2}\,\tan\,\frac{x}{2}\,\right)\right)\,\bigg|_0^{\frac{\pi}{2}}\,
\\
&=\;-\,\alpha\,
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/7232d81b7d7fd14442cf6e4203a9ee25.png)